On the Ellipse page we looked at the definition and some of the simple properties of the ellipse, but here we look at how to more accurately calculate its perimeter.
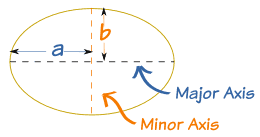 |
PerimeterRather strangely, the perimeter of an ellipse is very difficult to calculate!There are many formulas, here are a few interesting ones: |
Approximation 1
This approximation will be within about 5% of the true value, so long as a is not more than 3 times longer than b (in other words, the ellipse is not too "squashed"):
Approximation 2
The famous Indian mathematician Ramanujan came up with this better approximation:Infinite Series 1
This in an exact formula, but it requires an "infinite series" of calculations to be exact, so in practice you still only get an approximation.Firstly you must calculate e (the "eccentricity", not Euler's number "e"):
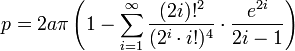
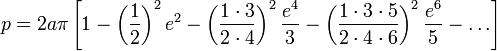
Infinite Series 2
But my favorite exact formula (because it gives a very close answer after only a few terms) is as follows:Firstly you must calculate "h":
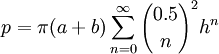
No comments:
Post a Comment